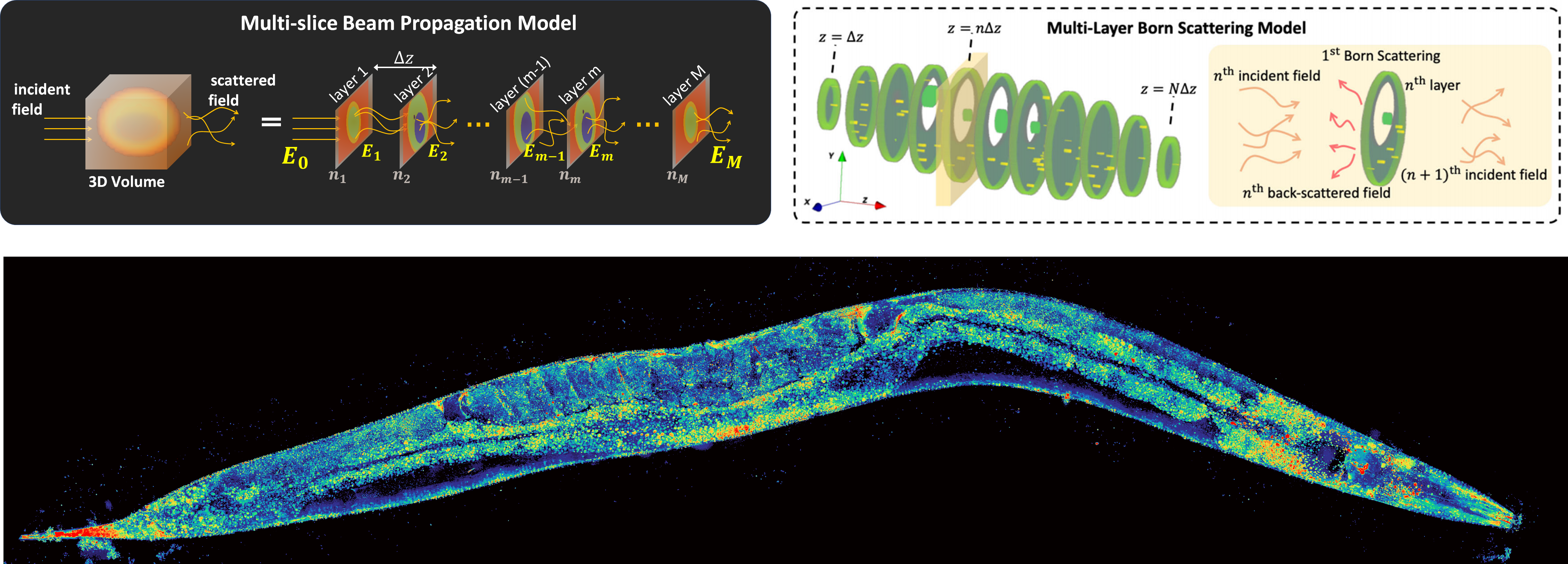
Multi-slice beam propagation

Provides Matlab code for the multi-slice beam propagation scatting model for 3D refractive-index reconstruction of multiple-scattering objects.

Multi-layer Born

Provides Python code for the multi-layer Born scattering model for 3D phase-contrast optical diffraction tomography.

Please cite as:

Shwetadwip Chowdhury, Michael Chen, Regina Eckert, David Ren, Fan Wu, Nicole Repina, and Laura Waller, “High-resolution 3D refractive index microscopy of multiple-scattering samples from intensity images,” Optica 6, 1211-1219 (2019)

Please cite as:

Michael Chen, David Ren, Hsiou-Yuan Liu, Shwetadwip Chowdhury, and Laura Waller, “Multi-layer Born multiple-scattering model for 3D phase microscopy,” Optica 7, 394-403 (2020)

Physics-based learning demonstration

The goal of this tutorial is to explain step-by-step how to implement physics-based learning for the rapid prototyping of a computational imaging system. We provide a basic overview of physics-based learning, the construction of a physics-based network, and its reduction to practice. Specifically, we advocate exploiting the auto-differentiation functionality twice, once to build a physics-based network and again to perform physics-based learning. Thus, the user need only implement the forward model process for their system, speeding up prototyping time. We provide an open-source Pytorch implementation of a physics-based network and training procedure for a generic sparse recovery problem.

Please cite as:

Michael Kellman, Michael Lustig, and Laura Waller, “How to do Physics-Based Learning,” arXiv:2005.13531 (2020)

Physics-based learning for lensless imaging

This page provides an example of an unrolled, physics-based network for lensess imaging reconstructions, using the alternating direction method of multiplers (ADMM) as the foundation of a physics-based network. In addition, a large dataset of 25,000 aligned lensless (DiffuserCam) and lensed images are provided.  These can be used to try out different learning-based inverse algorithms.

Please cite as:

Kristina Monakhova, Joshua Yurtsever, Grace Kuo, Nick Antipa, Kyrollos Yanny, and Laura Waller, “Learned reconstructions for practical mask-based lensless imaging,” Opt. Express 27, 28075-28090 (2019)

DiffuserCam reconstruction algorithm

Matlab code implements the alternating direction method of multipliers (ADMM) reconstruction algorithm for recovering images from diffuser-based lensless cameras. The algorithm solves an iterative least-squares problem to recover either 2D pictures or 3D data cubes from DiffuserCam raw data. Sample DiffuserCam data is provided.

Please cite as:

Nick Antipa, Grace Kuo, Reinhard Heckel, Ben Mildenhall, Emrah Bostan, Ren Ng, and Laura Waller, “DiffuserCam: lensless single-exposure 3D imaging,” Optica 5, 1-9 (2018)

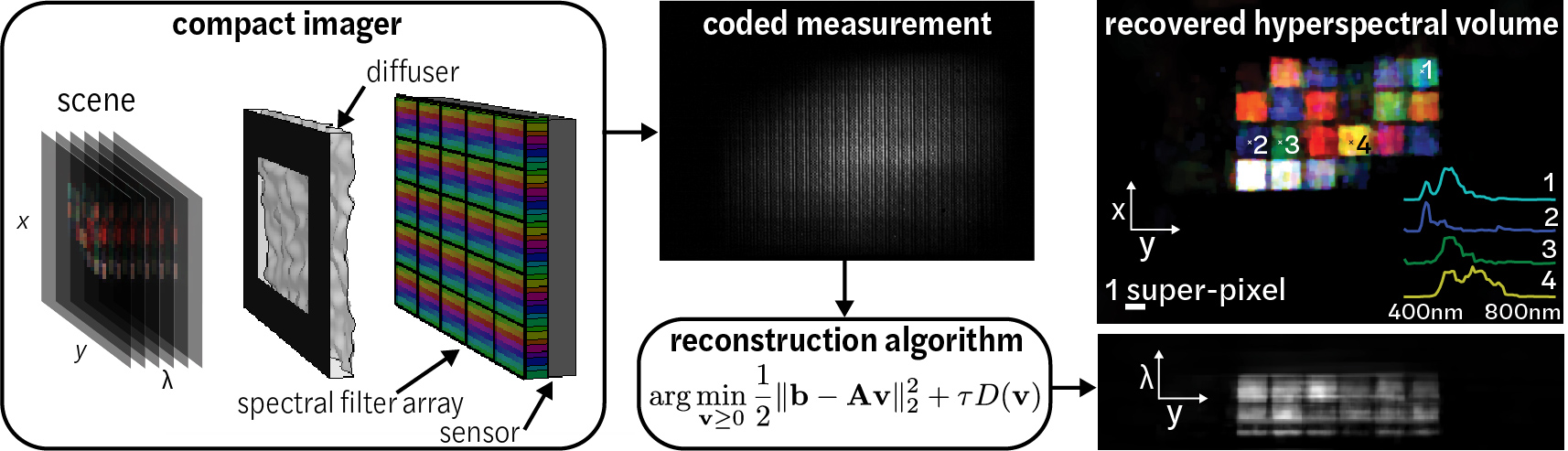
Spectral DiffuserCam reconstruction algorithm

Python and Matlab code implements the Fast Iterative Shrinkage Thresholding Algorithm (FISTA) for recovering images from a hyperspectral diffuser-based lensless cameras. The algorithm solves an iterative compressive-sensing-based reconstruction problem to recover a 3D hyperspectral data cube from Spectral DiffuserCam raw data. Sample Spectral DiffuserCam data is provided.

Please cite as:

Kristina Monakhova; Kyrollos Yanny; Neerja Aggarwal; Laura Waller: Spectral DiffuserCam: lensless snapshot hyperspectral imaging with a spectral filter array. Optica, 7 (10), pp. 1298–1307, 2020. 

Pycro-manager

Pycro-Manager enables Python control of Micro-Manager (an open-source microscopy control software) as well as providing a simple interface for the development of customized experiments using complex, automated microscopes. It is built to handle the requirements of modern, data-intensive microscopy, and it provides capabilities for integrating real-time image processing for adaptive experiments. It is compatible with hundreds of microscope components and full microscopes.

Please cite as:

Pinkard, H., Stuurman, N., Ivanov, I.E. et al. Pycro-Manager: open-source software for customized and reproducible microscope control. Nat Methods 18, 226–228 (2021). https://doi.org/10.1038/s41592-021-01087-6 

High content speckle structured illumination microscopy

Provides Matlab and Python implementations of a coherent/fluorescent structured illumination microscopy algorithm with random speckle illumination.

Please cite as:

Li-Hao Yeh, Shwetadwip Chowdhury, and Laura Waller, “Computational structured illumination for high-content fluorescence and phase microscopy,” Biomed. Opt. Express 10, 1978-1998 (2019) 

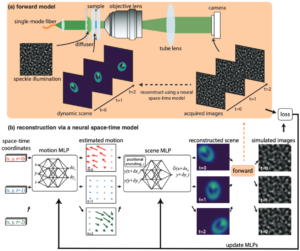
Structured illumination microscopy of dynamic samples

Provides Python code implementing the gradient descent solver for the neural space-time model used in the Speckle Flow SIM method. Speckle Flow SIM is a new structured illumination microscopy (SIM) technique that uses static patterned illumination on a dynamic scene and models the space-time relationship to super-resolve the dynamic scene.

Please cite as:

Ruiming Cao, Fanglin Linda Liu, Li-Hao Yeh, and Laura Waller, “Dynamic Structured Illumination Microscopy with a Neural Space-time Model,” 2022 IEEE International Conference on Computational Photography (ICCP), 2022, pp. 1-12 

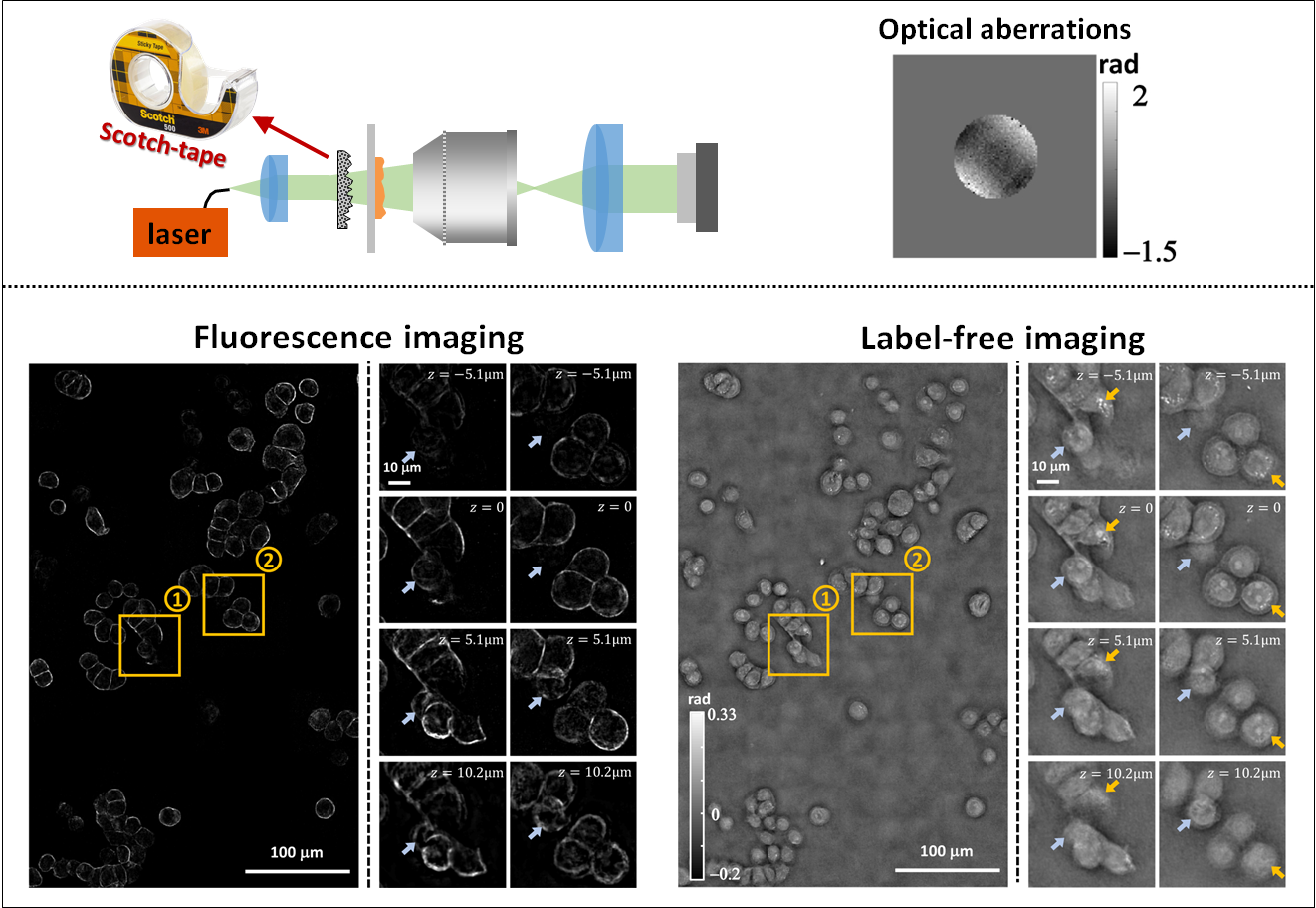
Quantitative Differential Phase Contrast (DPC) phase imaging with LED array (with Aberration Correction)

The code provides the option to solve the DPC phase retrieval problem using two different algorithms.

DPC Quantitative Phase Microscopy:
Matlab and Python codes implement a Tikhonov deconvolution based phase reconstruction algorithm from multi-axis DPC data. Images should be captured with LED array illumination or other switchable light sources using four halves of the brightfield circle on in each image. The transfer functions are calculated according to the Weak Object Transfer Function and the absorption and phase are solved with a least squares algorithm.

**Run the “main_dpc.m” under matlab_code folder and set the variable “aberration_correction” to “false”, or open the “main_dpc.ipynb” jupyter notebook under python_code folder.

DPC with Aberration Correction:
Matlab code implements a joint estimation algorithm for complex-field and pupil aberration reconstruction using a DPC dataset. This requires data with a combination of images under DPC or partially spatially coherent illuminations and spatially coherent illuminations. Minimum data of 3 DPC images and 1 on-axis spatially coherent image are provided as an example in the code. In each iteration, the code solves two sub optimization problems, including conventional DPC reconstruction with regularization and pupil aberration recovery. For the pupil aberration recovery, we adopt the L-BFGS method implemented in the open source optimization package, minFunc.

1. Download the minFunc package (https://www.cs.ubc.ca/~schmidtm/Software/minFunc.html).
2. Run the “main_dpc.m” under matlab_code folder and set the variable “aberration_correction” to “true”.

Please cite as:
L. Tian, L. Waller, Quantitative differential phase contrast imaging in an LED array microscope, Opt. Express 23, 11394-11403 (2015).
Z. F. Phillips, M. Chen, and L. Waller, Single-shot quantitative phase microscopy with color-multiplexed differential phase contrast (cDPC). PLOS ONE 12(2): e0171228 (2017).
Michael Chen, Zachary F. Phillips, and Laura Waller, “Quantitative differential phase contrast (DPC) microscopy with computational aberration correction,” Opt. Express 26, 32888-32899 (2018).

3D Quantitative Differential Phase Contrast (DPC) phase imaging with LED array

This repository provides Matlab and Python codes that implement a 3D refractive index reconstruction algorithm using 3D DPC through focus intensity measurements. Images should be captured with an LED array illumination or other switchable light sources, generating three(or more) half circular(or half annular) patterns. The 3D Weak Object Transfer Functions(WOTFs) are calculated according to the source patterns, pupil function, and the defocus step size. Finally, 3D refractive index are solved after a 3D deconvolution process. As in 2D DPC case, a least squares algorithm with Tikhonov regularization is implemented. Alternatively, deconvolution with total variation(TV) regularization and non-negativity constraint further mitigates artifacts based on a-priori knowledge of the object. GPU codes are available if hardware allows, which largely reduces computation time. In Python codes, we use ArrayFire library and its python wrapper for GPU processing implementation.

**Run the “main_3ddpc.m” under matlab_code folder, or open the “main_3ddpc.ipynb” jupyter notebook under python_code folder.

Please cite as:
[1] M. Chen, L. Tian and L. Waller, 3D differential phase contrast microscopy, Biomed. Opt. Express 7(10), 3940-3950 (2016).
[2] M. Chen and L. Waller, 3D Phase Microscopy with Coded Illumination, Biomed. Optics in the Life Sciences Congress:Novel Techniques in Microscopy, NM2C.2 (2017).

Data-driven design for Fourier ptychographic microscopy

Want to learn the experimental design for your computational imaging system? Checkout our code/datasets here to learn the best LED patterns for Fourier ptychographic microscopy. Here, we provide an implementation of multiplexed Fourier ptychography in python/pytorch for learning the experimental design.

Please cite as:

Michael Kellman, Emrah Bostan, Michael Chen, and Laura Waller, “Data-Driven Design for Fourier Ptychographic Microscopy,” IEEE International Conference for Computational Photography. 10.1109/ICCPHOT.2019.8747339 (2019).

Michael Kellman, Emrah Bostan, Nicole Repina, and Laura Waller, “Physics-based Learned Design: Optimized Coded-Illumination for Quantitative Phase Imaging,” IEEE Transactions on Computational Imaging. 10.1109/TCI.2019.2905434 (2019).

Illumination angle self-calibration in Fourier ptychography

Matlab code implementation of circle-finding algorithm to calibrate the angles of illumination for brightfield images and extend the calibration to darkfield images. Circular edge detection image processing is done on the Fourier transform of the data to calibrate the brightfield illumination directly. Python code implementation of spectral correlation calibration method inside the Fourier ptychography algorithm. The angles are iteratively refined within the FPM algorithm by correlating overlapping spectra. Sample data is provided.

Please cite as:

Regina Eckert, Zachary F. Phillips, and Laura Waller, “Efficient illumination angle self-calibration in Fourier ptychography,” Appl. Opt. 57, 5434-5442 (2018)

Fourier ptychography reconstruction algorithm with quasi-Newton second-order optimization

Matlab code implements Fourier ptychography reconstruction algorithm from a set of images captured under different illumination angles (e.g. in an LED array microscope), using either sequential or multiplexed coded illumination. The algorithm simultaneously estimates the complex object function (amplitude + phase) withhigh resolution (defined by objective NA+illumination NA) and the pupil function (aberrations). It implements a sequential quasi-Newton’s method with Tikhonov (L2) regularization.

Please cite as:

L. Tian, X. Li, K. Ramchandran, and L. Waller, “Multiplexed coded illumination for Fourier ptychography with an LED array microscope,” Biomedical Optics Express 5, 2376-2389 (2014).

(Dataset) LED array 2D Fourier ptychography

This dataset (may take a long time to download!) contains images from 293 different LED illumination angles up to NA=0.5, captured with a 4x 0.1 NA objective. Fourier ptychography thus enables ~0.6 NA (our reconstruction is here). We use an Adafruit LED array placed ~6cm above the sample on a Nikon TE300 inverted microscope (more experimental parameters in text file). The sample is a dog stomach cardiac region histology sample.

Please cite as: L. Tian, X. Li, K. Ramchandran, L. Waller, Biomedical Optics Express 5(7), 2376-2389 (2014).

L. Tian, Z. Liu, L. Yeh, M. Chen, Z. Jingshan, L. Waller, Optica 2(10), 904-911 (2015).

More datasets:

• USAF resolution test target
• In-vitro HeLa cancer cells
• Fixed U2OS cells (our reconstruction is here)

(Dataset) 3D Fourier ptychography

Images from sequential LED illumination up to 0.41 NA, using a 4x objective (0.1 NA). We achieved resolution corresponding to NA~0.5 with a multiple scattering multislice model that combines 3D light field refocusing with FPM to achieve super resolution in both lateral (x,y) and axial (z) dimensions.

Please cite as: L. Tian, L. Waller, 3D intensity and phase imaging from light field measurements in an LED array microscope, Optica 2, 104-111 (2015).

More datasets:

• two stacked USAF resolution targets
• spiral algae biological sample

2D phase retrieval from coherent defocus stack via nonlinear optimization

This code is for recovering complex field at focus (phase and amplitude) from a coherent defocus stack. The defocus stack includes multiple intensity images, which are measurements of through-focus coherent complex fields. It could be measured on a microscope by changing focus distance.

The reconstruction method in the code obtains an estimated complex field at focus by solving a nonlinear optimization problem. The optimization problem minimizes the mean squared error between the measured defocus stack and the predicted measurement, which is obtained by propagating the complex field at focus. The nonlinear optimization problem is solved with a modified Gauss-Newton method.

Please cite as:

J. Zhong, L. Tian, P. Varma and L. Waller, “Nonlinear Optimization Algorithm for Partially Coherent Phase Retrieval and Source Recovery,” in IEEE Transactions on Computational Imaging, vol. 2, no. 3, pp. 310-322, Sept. 2016.

2D phase retrieval from partially coherent defocus stack via nonlinear optimization

This code is used to recover phase and source for partially coherent defocus stack by nonlinear optimization.

Please cite as:

J. Zhong, L. Tian, P. Varma and L. Waller, “Nonlinear Optimization Algorithm for Partially Coherent Phase Retrieval and Source Recovery,” in IEEE Transactions on Computational Imaging, vol. 2, no. 3, pp. 310-322, Sept. 2016.

(Dataset) Phase from defocus cheek cell

This 68.2 MB image dataset contains a stack of 129 through-focus images from a Nikon TE300 microscope, captured with a piezo axial motion stage (Thorlabs PZ). Experimental parameters are listed in a separate text file included in the zip file download. The sample is unstained cheek cells from Jingshan Zhong’s mouth, placed on a microscope slide and sealed with a coverslide. This represents nearly a pure phase object, though there are some small specks of amplitude variation.

Please cite as: Z. Jingshan, R. Claus, J Dauwels, L. Tian, L. Waller, Optics Express 22(9), 10661-10674 (2014).

Light field refocusing and 3D differential phase contrast on LED array microscope:

Matlab code implements the popular ‘shift-and-add’ light field digital refocusing algorithm. The code is designed for processing data captured by sequentially turning on an array of illumination angles on our LED array microscope. It then splits the data based on illumination angles according to the differential phase contrast (DPC) method to compute the phase gradient information of the sample. The same algorithms can be also used for lenslet-based light field microscope.

Please cite as:
L. Tian, J. Wang, L. Waller, 3D differential phase contrast microscopy with computational illumination using an LED array, Opt. Lett. 9, 1326 – 1329 (2014).

Phase from defocus GUI:

This Matlab based phase recovery GUI provides a platform for implementing various TIE-based methods and iterative phase retrieval on a stack of through-focus intensity images. Input stack can be a 3D Matlab matrix (*.mat) or a sequence of tiff images (registration GUI included). Defocus steps need not be linearly spaced. The user can choose between standard TIE, higher order TIE [1], iterative TIE [2], Gaussian Process TIE [3] or the Gerchberg-Saxton iterative method for large defocus distances (see Fienup 1982).

Please cite as: G. Gunjala, L. Waller, Open Source PhaseGUI, UC Berkeley (2014)
[1] L. Waller, L. Tian, G. Barbastathis, Optics Express 18(12), 12552-12561 (2010).
[2] A. Shanker, L. Tian, M. Sczyrba, B. Connolly, A. Neureuther, L. Waller, Applied Optics (2014).
[3] Z. Jingshan, R. Claus, J Dauwels, L. Tian, L. Waller, Optics Express 22(9), 10661-10674 (2014).

CalOptrics GPU toolbox:

CalOptrics is an open source fast and easy-to-use C++ library for CUDA-based GPU computing of basic functions used in computational optical imaging. It uses an array-based function set which makes programming with CUDA easier than programming raw CUDA code. Underneath the hood, CalOptrics is powered by the Thrust, Cusp, and other CUDA open source libraries and designed using Object-oriented and abstraction techniques like interfaces to make modifications to raw lower-level implementations simple and quick. The design also makes it easy to implement a non-CUDA version like OpenCL to be used in this library.

Please cite as: D. Ramalingam, L. Waller, CalOptrics Open Source, UC Berkeley (2014).